8.25. Compute Feature Face Curvature

Group (Subgroup)

Surface Meshing (Curvature)

Description

This Filter calculates principal direction vectors and the principal curvatures, and optionally the mean and Gaussian curvature, for each Triangle in a Triangle Geometry using the technique in [1]. The groups of Triangles over which to compute the curvatures is determines by the Features they are associated, denoted by their Face Labels. The curvature information will be stored in a Face Attribute Matrix.

Principal Curvatures 1 and 2 are the κ ₁ and κ ₂ from [1] and are the eigenvalues from the Wiengarten matrix. The Principal Directions 1 and 2 are the eigenvectors from the solution to the least squares fit algorithm. The Mean Curvature is (κ ₁ + κ ₂ ) / 2, while the Gaussian curvature is (κ ₁ * κ ₂ ).

The values of the principal directions can have their signs flipped. They are calculated using eigenvectors which are unique up to a sign.

Note: Computing the Weingarten matrix values is an experimental feature, and there is no guarantee at this time that the values are correct.

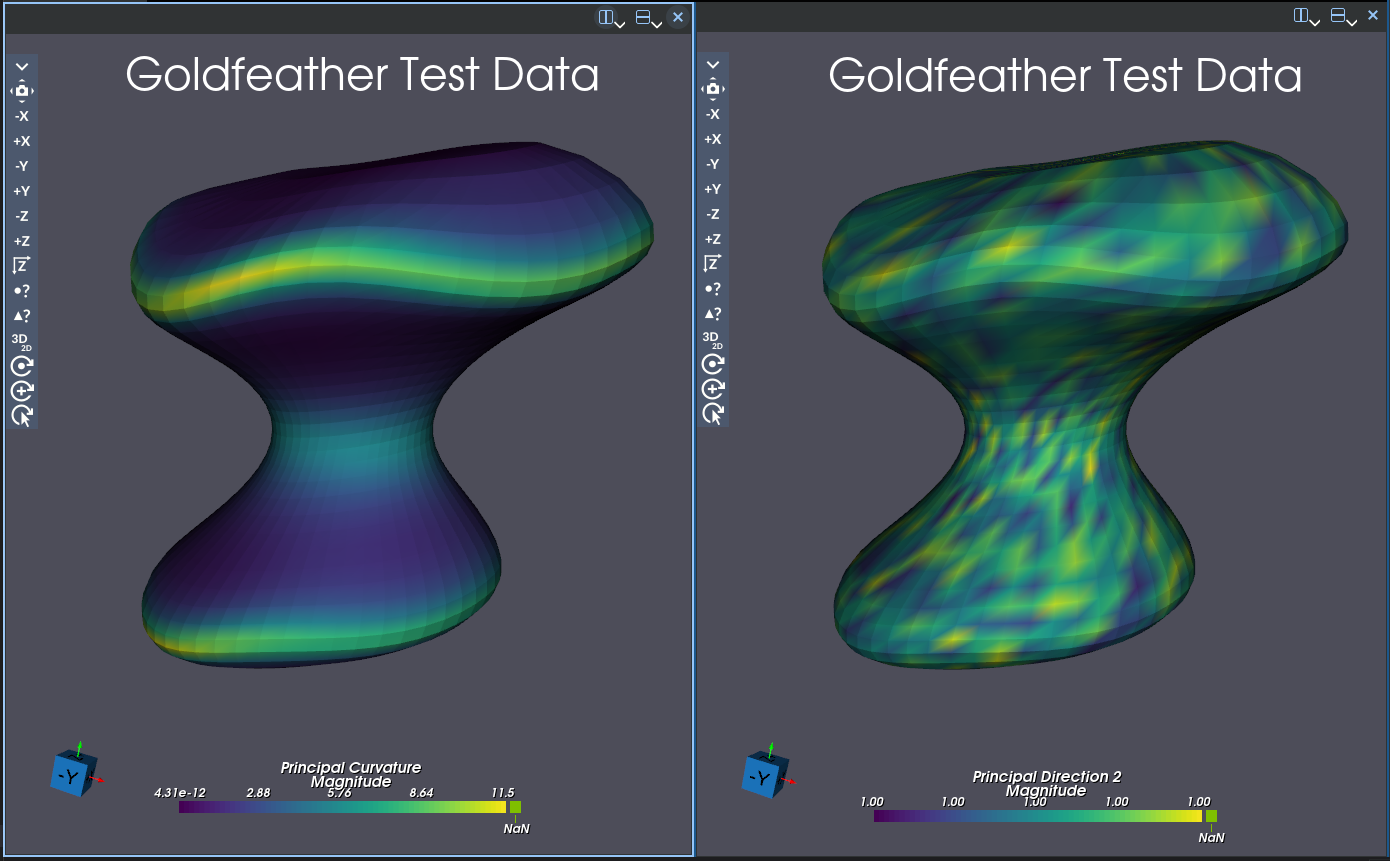@image latex FeatureFaceCurvatureFilter.png “Curvature Coloring of a Feature” width = 6in

Ring Neighbor Schematic

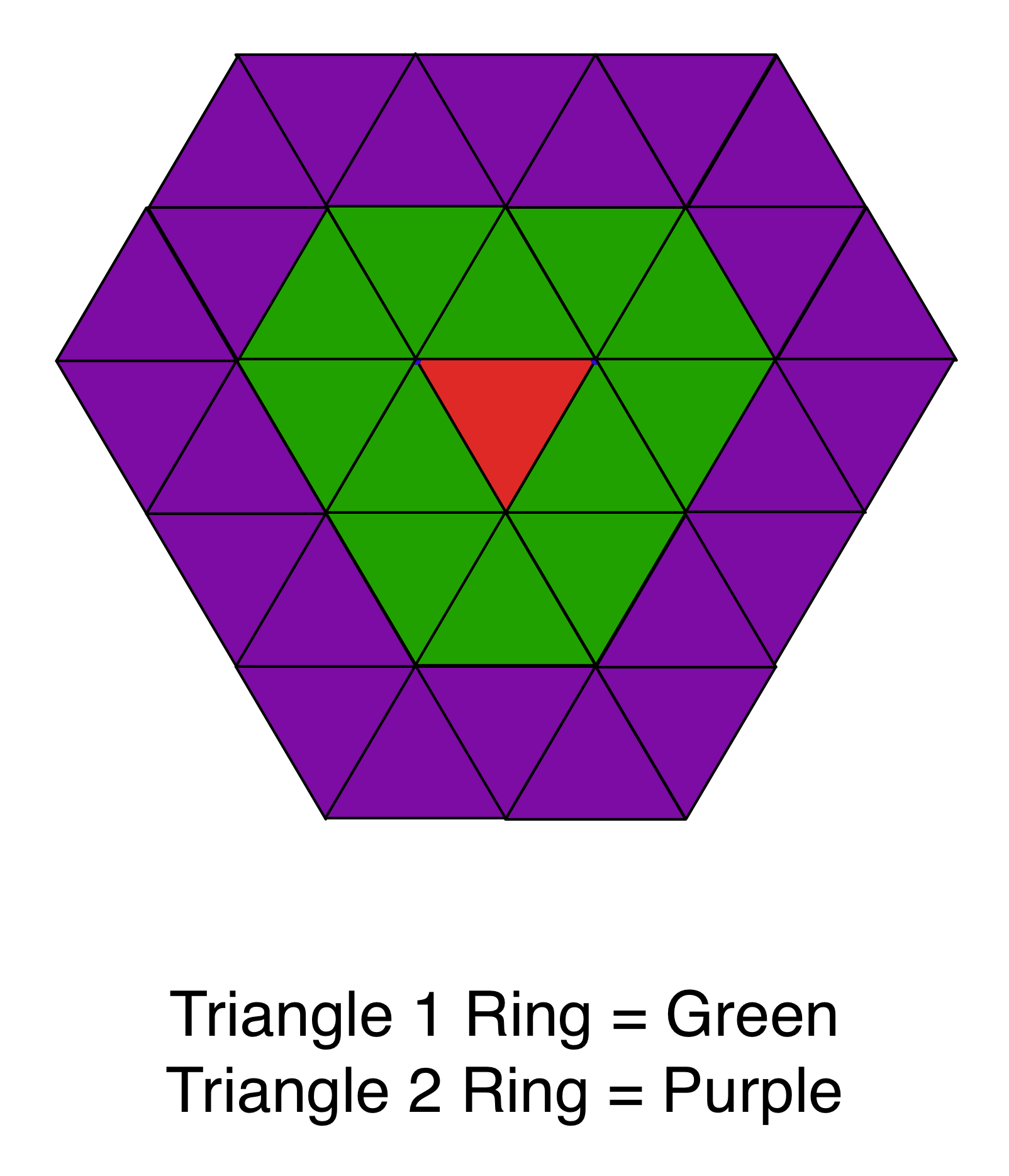
Parameter Notes:

• The “Feature Face Ids” input data can be computed from the “Compute Triangle Face Ids” filter

• The “Face Normals” input data can be computed from the “Compute Triangle Normals” filter

• The “Face Centroids” input data can be computed from the “Compute Triangle Centroids” filter

Input Parameter(s)

Parameter Name	Parameter Type	Parameter Notes	Description
Triangle Geometry	Geometry Selection	Triangle	The input Triangle Geometry to compute the curvature values
Neighborhood Ring Count	Scalar Value	Int32	The number of ring neighbors to use
Compute Principal Direction Vectors	Bool		Compute the Principal Direction Vectors
Compute Gaussian Curvature	Bool		Compute the Gaussian Curvature values
Compute Mean Curvature	Bool		Compute the Mean Curvature values
Compute Weingarten Matrix	Bool		Compute the Weingarten Matrix values
Use Face Normals for Curve Fitting	Bool		Use the face normals for curve fitting.

Input Triangle Face Data

Parameter Name	Parameter Type	Parameter Notes	Description
Face Attribute Matrix	AttributeMatrixSelection		The AttributeMatrix that holds the triangle face data.
Face Labels	Array Selection	Allowed Types: int32 Comp. Shape: 2	The DataPath to the ‘Face Labels’ DataArray
Feature Face Ids	Array Selection	Allowed Types: int32 Comp. Shape: 1	The DataPath to the ‘FeatureIds’ DataArray
Face Normals	Array Selection	Allowed Types: float64 Comp. Shape: 3	The DataPath to the ‘Feature Normals’ DataArray
Face Centroids	Array Selection	Allowed Types: float64 Comp. Shape: 3	The DataPath to the ‘Face Centroids’ DataArray

Output Face Data

Parameter Name	Parameter Type	Parameter Notes	Description
Principal Curvature 1	ArrayCreation		Output DataPath to hold the ‘Principal Curvature 1’ values
Principal Curvature 2	ArrayCreation		Output DataPath to hold the ‘Principal Curvature 2’ values
Principal Direction 1	ArrayCreation		Output DataPath to hold the ‘Principal Direction 1’ values
Principal Direction 2	ArrayCreation		Output DataPath to hold the ‘Principal Direction 2’ values
Gaussian Curvature	ArrayCreation		Output DataPath to hold the ‘Gaussian Curvature’ values
Mean Curvature	ArrayCreation		Output DataPath to hold the ‘Mean Curvature’ values
Weingarten Matrix	ArrayCreation		Output DataPath to hold the ‘Weingarten Matrix’ values

References

[1] J. Goldfeather, V. Interrante, “A Novel Cubic-Order Algorithm for Approximating Principal Direction Vectors”, ACM Transactions on Graphics 2004, 23(1), pp. 45 - 63.

Example Pipelines

• Pipelines -> SimplnxCore -> Compute_Feature_Face_Curvature

• Pipelines -> SimplnxCore -> Compute_Feature_Face_Curvature_2

License & Copyright

Please see the description file distributed with thisPlugin

DREAM3D-NX Mailing Lists

If you need more help with aFilter, please consider asking your question on the DREAM3D-NX Users Google group!