10.16. Compute GBCD (Metric-Based Approach)

Group (Subgroup)

Statistics (Crystallographic)

Description

This Filter computes a section through the five-dimensional grain boundary distirbution for a fixed misorientation. An example of such a section is shown in Fig. 1. Differently than Compute GBCD Filter, which uses a method based on partition of the boundary space into bins, this Filter implements an alternative metric-based approach described by K. Glowinski and A. Morawiec in Analysis of experimental grain boundary distributions based on boundary-space metrics, Metall. Mater. Trans. A 45, 3189-3194 (2014)

Metrics in the boundary space can be defined in a number of ways, but it is essential that two boundaries are close (distant) if they have similar (different) geometric features, and that symmetrically equivalent representations of boundaries are taken into consideration. Formally, the boundary space is a Cartesian product of the misorientation and boundary-normal subspaces. For computational reasons and because of considerably different resolutions in determinination of grain misorientation and boundary-plane parameters, it is convenient to use a separate metric in each subspace. With separate metrics, the procedure for computing distribution values for a selected misorientation has two stages. First, boundary segments with misorientations located not farther from the fixed misorientation than a limiting distance ρ_m are selected. In the second stage, the distribution is probed at evenly distributed normal directions (see Fig. 2), and areas of boundaries whose normals deviate from a given direction by less than ρ_p are summed. (The radii ρ_m and ρ_p should be tailored to resolution, amount, and quality of data and set.) Eventually, the obtained distribution is normalized in order to express it in the conventional units, i.e., multiples of the random distribution.

Image
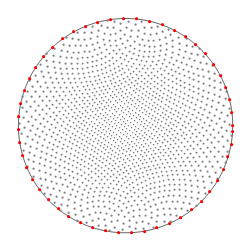
Fig. 2: End-points (drawn in stereographic projection) of sampling directions used for probing distribution values; the number of points here is about 1500. Additionally, distributions are probed at points lying at the equator (marked with red); this is helpful for some plotting software.

This Filter also calculates statistical errors of the distributions using the formula

ε = ( f n v )^1/2

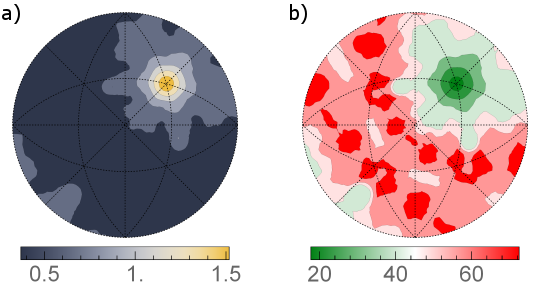
where ε is the relative error of the distribution function at a given point, f is the value of the function at that point, n stands for the number of grain boundaries (not the number of mesh triangles) in the considered network, and v denotes the volume restricted by ρ_m and ρ_p. The errors can be calculated either as their absolute values, i.e., ε × f (Fig. 3a) or as relative errors, i.e., 100% × ε (Fig. 3b). The latter are computed in a way that if the relative error exceeds 100%, it is rounded down to 100%.

Image

Format of Output Files

Output files are formatted to be readable by GMT plotting program. The first line contains the fixed misorientation axis and angle. Each of the remaining lines contains three numbers. The first two columns are angles (in degrees) describing a given sampling direction; let us denote them col₁ and col₂, respectively. The third column is either the value of the GBCD (in MRD) for that direction or its error (in MRD or %, depending on user’s selection). If you use other software, you can retrive spherical angles θ and φ of the sampling directions in the following way:

θ = 90° - col₁

φ = col₂

Then, the directions are given as [ sin θ × cos φ , sin θ × sin φ , cos θ ].

Feedback

In the case of any questions, suggestions, bugs, etc., please feel free to email the author of this Filter at kglowinski at ymail.com

Input Parameter(s)

Parameter Name	Parameter Type	Parameter Notes	Description
Phase of Interest	Scalar Value	Int32	Index of the Ensemble for which to compute GBCD; boundaries having grains of this phase on both its sides will only be taken into account
Fixed Misorientation	Vector of Float32 Values	Order=x,y,z,w	Axis-angle representation of the misorientation of interest. Angle value should be in degrees.
Limiting Distances	Choices		The max angles from within which boundary segments are selected for the misorientations and plane inclinations
Number of Sampling Points (on a Hemisphere)	Scalar Value	Int32	The approximate number of sampling directions
Exclude Triangles Directly Neighboring Triple Lines	Bool		If checked, only interiors of Faces are included in GBCD
Save Relative Errors Instead of Their Absolute Values	Bool		Whether or not to save the distribution errors as relative (if exceeds 100%, then rounded down) or absolute
Triangle Geometry	Geometry Selection	Triangle	The complete path to the triangle geometry

Input Triangle Geometry Vertex Data

Parameter Name	Parameter Type	Parameter Notes	Description
Node Types	Array Selection	Allowed Types: int8 Comp. Shape: 1	Specifies the type of node in the Geometry

Input Triangle Geometry Face Data

Parameter Name	Parameter Type	Parameter Notes	Description
Face Labels	Array Selection	Allowed Types: int32 Comp. Shape: 2	Specifies which Features are on either side of each Face
Face Normals	Array Selection	Allowed Types: float64 Comp. Shape: 3	Specifies the normal of each Face
Face Areas	Array Selection	Allowed Types: float64 Comp. Shape: 1	Specifies the area of each Face

Input Triangle Geometry Face Feature Data

Parameter Name	Parameter Type	Parameter Notes	Description
Feature Face Labels	Array Selection	Allowed Types: int32 Comp. Shape: 2	Specifies which original Features are on either side of each boundary Feature

Input Feature Data

Parameter Name	Parameter Type	Parameter Notes	Description
Average Euler Angles	Array Selection	Allowed Types: float32 Comp. Shape: 3	Three angles defining the orientation of the Feature in Bunge convention (Z-X-Z)
Phases	Array Selection	Allowed Types: int32 Comp. Shape: 1	Specifies to which phase each Feature belongs

Input Ensemble Data

Parameter Name	Parameter Type	Parameter Notes	Description
Crystal Structures	Array Selection	Allowed Types: uint32 Comp. Shape: 1	Enumeration representing the crystal structure for each Ensemble

Output Parameters

Parameter Name	Parameter Type	Parameter Notes	Description
Output Distribution File	FileSystemPath		The output distribution file path (extension .dat, GMT format)
Output Distribution Errors File	FileSystemPath		The output distribution errors file path (extension .dat, GMT format)

References

[1] K. Glowinski and A. Morawiec, Analysis of experimental grain boundary distributions based on boundary-space metrics, Metall. Mater. Trans. A 45, 3189-3194 (2014)

Example Pipelines

(05) SmallIN100 GBCD Metric.d3dpipeline

This pipeline depends on previous pipelines in the Small IN100 reconstruction pipeline series.

License & Copyright

Please see the description file distributed with this Plugin.

DREAM3D-NX Help

If you need help, need to file a bug report or want to request a new feature, please head over to the DREAM3DNX-Issues GitHub site where the community of DREAM3D-NX users can help answer your questions.